Sportka is a popular lottery in Czechia, with an average superjackpot over 100M CZK. What is the chance of winning the lottery? How much one loses by long-term betting? Today, we shall answer these questions, this time using R.
Ticket
A Sazka lottery ticket shown below contains 10 identical columns, each with numbers 1-49. In each round of Sportka, 6 distinct numbers are drawn from 1-49. Better selects 6 numbers in the column, the reward depends on how many chosen numbers were drawn.
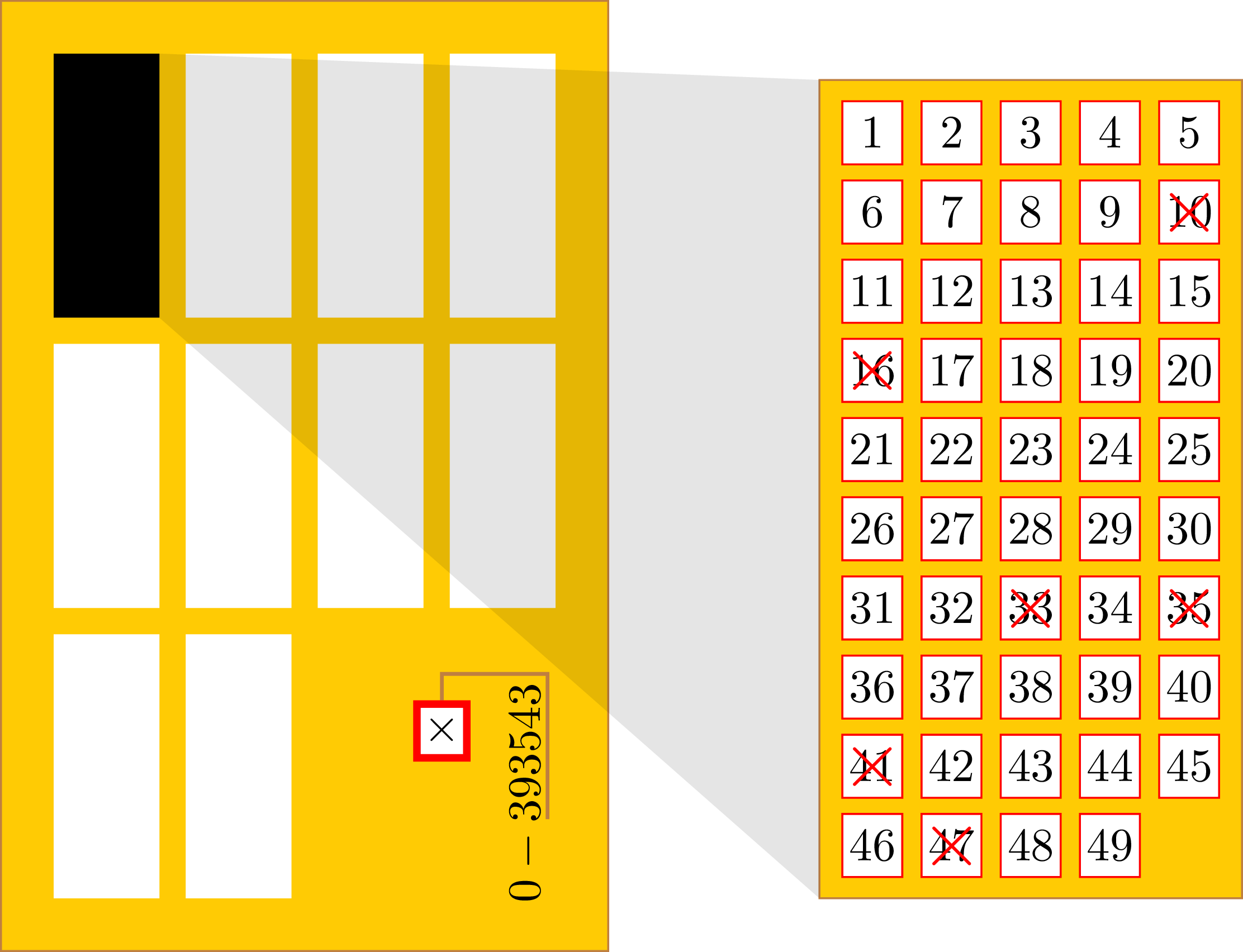
A bottom-right corner of each ticket contains a unique number. Apart from ticket identification, this number is also used for a supplementary game Šance. A 6-digit number is drawn, and the reward for Šance is based on length of matched suffix digits with the ticket identifier.
The ticket is used for 2 draws, each connected with different rewards. Sportka is played twice a week. As of 2023, the price for one column is 20 CZK, and the price for Šance is also 20 CZK.
There exists a similar blogpost modelling Sportka, but the modelling there is wrong.
Sportka
For simplicity, we assume a single lottery draw, and a single column bet. Playing sportka can be understood as blindly picking $6$ stones from a bag of $6$ black and $43$ white stones, and counting black stones in the pick.
Sportka follows hypergeometric distribution - a binomial distribution with replacement.
> Pr_sportka <- dhyper(0:6, 6, 49-6, 6)

The chance of perfect guess, $6$ out of $6$, is $7.15\cdot10^{-8}$. To put this number in a context - if everyone in Czechia bet a single column twice a week, there would be one lucky better every $34$ weeks on average.
> sum(Pr_sportka[1:3])
0.9813625
The chance of losing (i.e., reward $0$) is $98.1$%.
The probabilities can be alternatively estimated in a frequentist manner via simulation ($N=10^5$).
> library(plyr)
> set.seed(12345)
> bet <- sample(1:49, 6, replace=F)
> win <- replicate(100000, length(intersect(sample(1:49, 6), bet)))
> table(win) / length(win)
0 1 2 3 4
0.43781 0.41226 0.13187 0.01706 0.00100
Unfortunately, this method errs in probabilities of rare events, such as superjackpot.
> setNames(Pr_sportka, 0:6)
0 1 2 3 4 5 6
0.43597 0.41302 0.13238 0.01765 9.6862e-04 1.8441e-05 7.1511e-08
Dodatkové číslo
After drawing $6$ numbers, an additional number (dodatkové číslo) is drawn. Guessing this number increases reward given that 5/6 Sportka numbers are correctly guessed.
Guessing dodatkové číslo is led by Bernoulli distribution.
> Pr_dodatkove <- 1/(49-6)
0.02325581
Pořadí
The rewards are organized in "order" (pořadí), based on the count of numbers guessed.
Guessed |
Order |
Probability |
|---|---|---|
| 6/6 | 1. | $7.2\cdot10^{-8}$ |
| 5/6 + dodatkové | 2. | $4.3\cdot10^{-7}$ |
| 5/6 | 3. | $1.8\cdot10^{-5}$ |
| 4/6 | 4. | $9.7\cdot10^{-4}$ |
| 3/6 | 5. | $0.018$ |
Chance of 2. order means combining probabilities of 3. order and of guessing dodatkové číslo. As these are independent, we simply multiply them.
> Pr_sportka[6]*Pr_dodatkove
4.290674e-07
Tahy
Sportka is played in two independent draws (tahy). Each draw has different reward tables. Moreover, the table changes over time, so from now on, all the results depend on the reward table at the time.
I use rewards from 22nd December 2023.
> reward_tah1 <- c(0, 0, 0, 112, 630, 24283, 330520)
> reward_tah2 <- c(0, 0, 0, 117, 664, 47217, 330520)
> reward_poradi2 <- 730000
> reward_sance <- c(0, 50, 100, 10^3, 10^4, 10^5, 970000)
Average reward of Sportka
Average reward is computed as an expected value over the rewards.
> avg_reward_tah1 <- (
+ Pr_sportka %*% reward_tah1 +
+ Pr_sportka[6] * Pr_dodatkove * reward_poradi2)
> avg_reward_tah2 <- (
+ Pr_sportka %*% reward_tah2 +
+ Pr_sportka[6] * Pr_dodatkove * reward_poradi2)
> avg_reward_sportka <- avg_reward_tah1 + avg_reward_tah2 - 20
-12.71179
The average reward is $-12.7$ CZK. With the initial price $20$ CZK, this means a loss of $63.5$%.
Šance
Supplementary game Šance is based on guessing suffix of digits. Guessing the last k-digits is Bernoulli-distributed, with $p=10^{-k}$.
> Pr_sance <- 1/10^(1:6)
> Pr_sance <- c(1-sum(Pr_sance), Pr_sance)
The probability of winning anything is as follows.
> sum(Pr_sance[2:7])
0.111111
The average reward of Šance is computed as expectation over rewards. For the selected reward values, Šance has higher return than Sportka.
> avg_reward_sance <- Pr_sance %*% reward_sance
> avg_reward_sance - 20
-10.03
The average reward of Šance is $-10$ CZK. With initial price $20$ CZK, we get average loss $50$%.
Šance is less lossy than Sportka, and has much lower chance of losing (reward $0$).
Superjackpot
Reported rewards assume playing Sportka, or Šance separately.
If both games are playing together, better can win superjackpot, whose value is currently $151$M. Winning superjackpot requires
- winning 1. order, and
- winning at least one digit of Šance.
If a single column is bet, the ticket price is $40$, and the average reward is as follows.
> avg_reward <- (
+ avg_reward_sportka +
+ avg_reward_sance +
+ Pr_sportka[7] * sum(Pr_sance[2:7]) * 151000000 +
+ Pr_sportka[7] * sum(Pr_sance[2:7]) * 151000000)
> avg_reward - 40
-20.3
With average reward $-20.3$, the loss is $50.8$%.
Betting multiple columns
Another question is, whether it is long-term beneficial to bet multiple columns. Here we need to get a bit formal: we fill $N$ columns, where $y$ is the set with drawn values, and $x_i$ is the guess in $i^{\text{th}}$ column. $R(\cdot)$ is the reward function, and $\cap$ denotes set union.
The total reward sums up, when betting in multiple columns. The columns are chosen before revealing the results, there is no information exchange between the draws. Thus, each column can be assumed to be an independent draw from hypergeometric distribution.
$E_{x\sim X}\bigg[\sum_{i=1}^{N}R(x_i\cap y)\bigg]\stackrel{\perp}{=}\sum_{i=1}^{N}E_{x_i\sim X}\big[R(x_i\cap y)\big]\stackrel{\text{id}}{=}N\cdot E_{x\sim X}\big[R(x_i\cap y)\big]$
As Sportka tips are independent, average rewards / losses adds up. Betting multiple columns does not give any benefit, compared to betting a single column.
We can take a look at the probability of losing ticket (no win in any column) as a distribution of number of columns.

> 1 - sum(Pr_sportka[1:3])^10
0.1714964
A full ticket with $10$ filled columns costs $200$ CZK. The probability of not losing is $0.1714964$.
Conclusion
- Analyzed lottery games lead to average loss more than $50$%.
- Šance is less lossy than Sportka.
- Playing Šance along Sportka is less lossy than playing Sportka alone.
- Number of columns does not increase average reward.