Living in mountains, I get many opportunities to ask myself the most fundamental question: "Can a sheep herd be modelled similarly to fluid dynamics?" Today, we are gonna use cellular automaton to finally find the answer.
Observing sheep
For those who has never left the subway system of a metropolitan area, sheep tent to stick close to the herd, in order to stay safe.
"Following like a sheep" describes the herd movements pretty accurately.

As a result, a sheep herd on a large grass area behaves like a white liquid on green background, floating around gray rocks and cliffs.
Cellular automaton
Cellular automaton is a model of spatial interactions. Its typical application are fluid dynamics, meteorology, civil engineering, epidemiology, or ecology.
The model is a regular lattice of cells, each holding a state.
There is a handful of possible states; in our case, it will be empty, sheep, and later predator.
The model evolves over time, based on the neighborhood of each cell.
Apart from space, the model also captures time: typically, as a discrete axis, i.e., $0$, $1$, $2$, ..., along which the state of the model evolves. The change in state determines the interactions, and is defined regressively, from time $k$ to $k+1$.
Finally, we should address the elephant in the room. Yes, our sheep will be square-shaped.
Modelling the herd with cellular automaton
Let's have a large, grass area, decomposed into square segments. Each square is either empty, or has a square-shaped sheep standing on it. We initialize the space by randomly dropping sheep around the area.
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
# actors
EMPTY = 0
SHEEP = 1
TOURIST = 2
# randomly spread sheep around the area
rng = np.random.default_rng(12345)
area = rng.choice([EMPTY, SHEEP], size=(50, 50), p=[.95, .05])
print('Generated', np.sum(area == SHEEP), 'sheep.')
# plot the area
A = np.zeros((*area.shape, 3), dtype='uint8')
A[area == EMPTY] = [0, 128, 0]
A[area == SHEEP] = [255, 255, 255]
plt.imshow(A);
Generated 135 sheep.

Next, we get the sheep moving. For visualizing time-dependent heatmaps, we use pillow and store them in as GIF images.
Cellular automaton is defined via behavior of an individual. Individuals define the movement based on the current state, reacting to what happens in the neighborhood. In our case, we must define "the sheep logic".
Sheep logic
The schema below shows the logic of sheep. Sheep tries to run towards the local herd centroid. Later we will also introduce the tourists that sheep runs from and extend the sheep movements towards Moore.
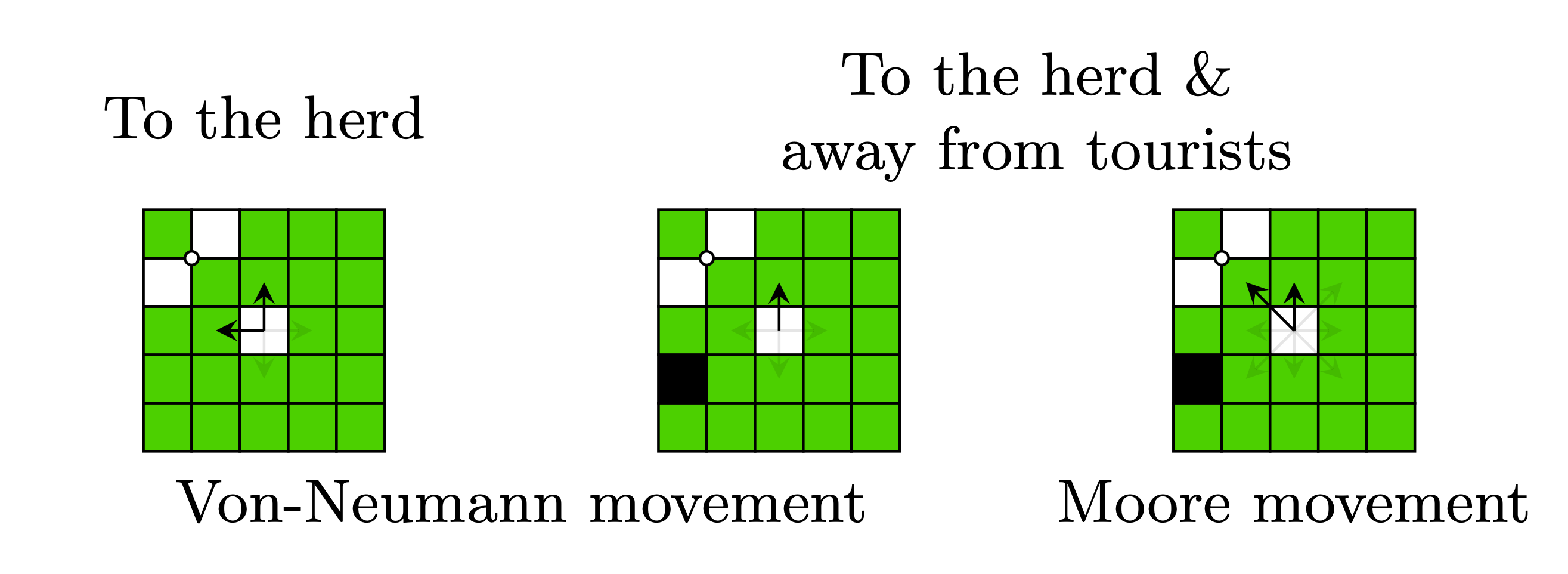
A sheep first estimates a herd centroid. Then it considers possible moves (up, down, left, right, stay), and weights them by the dot product with the vector towards the centroid. What this means is that directions getting the sheep towards the centroid get positive, larger score, and directions away from centroid get negative score.
Finally, the scores are converted to probabilities using the softmax function, and the direction is drawn randomly, according to the probabilities.
def score_to_direction(score):
# softmax score
p_sum = np.sum(np.exp(list(score.values())))
p = {k: np.exp(v) / p_sum for k, v in score.items()}
# draw randomly
direction = rng.choice(list(p.keys()), p=list(p.values()))
return direction
def sheep_logic(area_win, loc, glob, lim):
# sheep centroid
sheep = np.array(list(zip(*np.where(area_win == SHEEP))))
ctr = np.mean(sheep, axis=0) if len(sheep[0]) > 0 else np.array(loc)
# gravity score
score = {
tuple(k): np.array(k) @ (ctr - loc)
for k in [(-1, 0), (1, 0), (0, -1), (0, 1), (0, 0)]
}
# check
for direction, in_area in [
[(-1, 0), glob[0] > lim[0][0]],
[(0, -1), glob[1] > lim[0][1]],
[(+1, 0), glob[0] < lim[1][0]-1],
[(0, +1), glob[1] < lim[1][1]-1],
]:
# do not roam outside the area
if not in_area:
score[direction] = -np.inf
# the next square must be empty
elif area[x_glob+direction[0], y_glob+direction[1]] != EMPTY:
score[direction] = -np.inf
# direction according to score
return score_to_direction(score)
We test our function for $100$ time steps, on an area of $75\times75$ squares with $5%$ sheep. Each sheep only sees $15\times15$ pixels around it.
# initialize sheep area
rng = np.random.default_rng(12345)
area = rng.choice([EMPTY, SHEEP], size=(75, 75), p=[.95, .05])
# parameters
win_size = 15
clamp = lambda x, dim: np.clip(x, 0, area.shape[dim])
# run
frames = []
for step in range(50):
frame = np.zeros((*area.shape, 3), dtype='uint8')
for x_glob, y_glob in zip(*np.where((area == SHEEP))):
object_type = area[x_glob, y_glob]
# Moore View neighborhood
win_min = clamp(x_glob-win_size//2, 0), clamp(y_glob-win_size//2, 1)
win_max = clamp(x_glob+win_size//2+1, 0), clamp(y_glob+win_size//2+1, 1)
area_win = area[win_min[0]:win_max[0], win_min[1]:win_max[1]]
x_loc, y_loc = x_glob - win_min[0], y_glob - win_min[1]
# Sheep logic
direction = sheep_logic(area_win, [x_loc, y_loc], [x_glob, y_glob], [win_min, win_max])
# Add to frame
frame[area == EMPTY] = [0, 128, 0]
frame[area == SHEEP] = [255, 255, 255]
# Move
area[x_glob, y_glob] = EMPTY
area[x_glob+direction[0], y_glob+direction[1]] = object_type
frames.append(Image.fromarray(frame))
frames[0].save("image.gif", save_all=True, append_images=frames[1:])

The sheep cluster together, but nothing really pushes them into moving further. The sub-herds do not see each other, as their centroids are more than $7$ blocks apart.
Adding the tourists
Let us make it more interesting. Let's add tourists. Tourists run towards the sheep.
tourist_factor = .2 # factor controlling how much tourists run after the sheep
def tourist_logic(area_win, loc, glob, lim):
# sheep centroid
sheep = list(zip(*np.where(area_win == SHEEP)))
if len(sheep) > 0:
ctr = np.mean(sheep, axis=0)
else:
ctr = np.array(loc)
# gravity score (towards sheep)
score = {
tuple(k): np.array(k) @ (ctr - loc)
for k in [(-1, 0), (1, 0), (0, -1), (0, 1), (0, 0)]
}
# check
for direction, in_area in [
[(-1, 0), glob[0] > lim[0][0]],
[(0, -1), glob[1] > lim[0][1]],
[(+1, 0), glob[0] < lim[1][0]-1],
[(0, +1), glob[1] < lim[1][1]-1],
]:
# do not roam outside the area
if not in_area:
score[direction] = -np.inf
# the next square must be empty
elif area[x_glob+direction[0], y_glob+direction[1]] != EMPTY:
score[direction] = -np.inf
score[direction] *= tourist_factor
# direction according to score
return score_to_direction(score)
Sheep are afraid of tourists, and run away from them.
fear_factor = 10 # how much are sheep afraid of tourists
def sheep_logic(area_win, loc, glob, lim):
# sheep centroid
ctr = np.mean(list(zip(*np.where(area_win == SHEEP))), axis=0)
# gravity score (towards sheep centroid)
score_sheep = {
tuple(k): np.array(k) @ np.array(ctr - loc)
for k in [(-1, 0), (1, 0), (0, -1), (0, 1), (0, 0)]
}
# anti-gravity score (from tourists)
tourists = np.array(list(zip(*np.where(area_win == TOURIST))))
score_tourist = {
tuple(k): min([*[
np.array(k) @ (np.array(tourist) - loc)
for tourist in tourists
], 0])
for k in [(-1, 0), (1, 0), (0, -1), (0, 1), (0, 0)]
}
if any([np.sum(np.abs(tourist - loc)) < 3 for tourist in tourists]):
score_tourist[(0, 0)] = np.inf # don't stay still when people are around
# combine both scores
score = {
k: score_sheep[k] - fear_factor * score_tourist[k]
for k in score_sheep
}
# check
for direction, in_area in [
[(-1, 0), glob[0] > lim[0][0]],
[(0, -1), glob[1] > lim[0][1]],
[(+1, 0), glob[0] < lim[1][0]-1],
[(0, +1), glob[1] < lim[1][1]-1],
]:
# do not roam outside the area
if not in_area:
score[direction] = -np.inf
# the next square must be empty
elif area[x_glob+direction[0], y_glob+direction[1]] != EMPTY:
score[direction] = -100
# direction according to score
return score_to_direction(score)
We plug both together. We populate $5%$ with sheep, and $0.2%$ with tourists.
# initialize sheep area
rng = np.random.default_rng(12345)
area = rng.choice([EMPTY, SHEEP, TOURIST], size=(75, 75), p=[.949, .05, .001])
# parameters
win_size = 15
# run
frames = []
for step in range(50):
frame = np.zeros((*area.shape, 3), dtype='uint8')
for x_glob, y_glob in zip(*np.where(area != EMPTY)):
object_type = area[x_glob, y_glob]
# Moore View neighborhood
win_min = clamp(x_glob-win_size//2, 0), clamp(y_glob-win_size//2, 1)
win_max = clamp(x_glob+win_size//2+1, 0), clamp(y_glob+win_size//2+1, 1)
area_win = area[win_min[0]:win_max[0], win_min[1]:win_max[1]]
x_loc, y_loc = x_glob - win_min[0], y_glob - win_min[1]
# Sheep logic
if object_type == SHEEP:
direction = sheep_logic(area_win, [x_loc, y_loc], [x_glob, y_glob], [win_min, win_max])
elif object_type == TOURIST:
direction = tourist_logic(area_win, [x_loc, y_loc], [x_glob, y_glob], [win_min, win_max])
# Add to frame
frame[area == EMPTY] = [0, 128, 0]
frame[area == SHEEP] = [255, 255, 255]
# Move
area[x_glob, y_glob] = EMPTY
area[x_glob+direction[0], y_glob+direction[1]] = object_type
frames.append(Image.fromarray(frame))
frames[0].save("image.gif", save_all=True, append_images=frames[1:])

Nice! The sheep are (moderately) avoiding the tourists, which breaks the clusters.
Moves like Moore
Final modification is to replace the von Neumann neighborhood movement with Moore movement.
def tourist_logic(area_win, loc, glob, lim):
# sheep centroid
sheep = list(zip(*np.where(area_win == SHEEP)))
if len(sheep) > 0:
ctr = np.mean(sheep, axis=0)
else:
ctr = np.array(loc)
# gravity score (towards sheep)
score = {
tuple(k): np.array(k) @ (ctr - loc)
for k in [(-1, 0), (1, 0), (0, -1), (0, 1), (1, 1), (1, -1), (-1, 1), (-1, -1), (0, 0)]
}
# check
for direction, in_area in [
[(-1, 0), glob[0] > lim[0][0]],
[(0, -1), glob[1] > lim[0][1]],
[(+1, 0), glob[0] < lim[1][0]-1],
[(0, +1), glob[1] < lim[1][1]-1],
[(-1, +1), (glob[0] > lim[0][0]) & (glob[1] < lim[1][1]-1)],
[(+1, -1), (glob[0] < lim[1][0]-1) & (glob[1] > lim[0][1])],
[(-1, -1), (glob[0] > lim[0][0]) & (glob[1] > lim[0][1])],
[(+1, +1), (glob[0] < lim[1][0]-1) & (glob[1] < lim[1][1]-1)],
]:
# do not roam outside the area
if not in_area:
score[direction] = -np.inf
# the next square must be empty
elif area[x_glob+direction[0], y_glob+direction[1]] != EMPTY:
score[direction] = -np.inf
score[direction] *= tourist_factor
# direction according to score
return score_to_direction(score)
def sheep_logic(area_win, loc, glob, lim):
# sheep centroid
sheep = np.array(list(zip(*np.where(area_win == SHEEP))))
ctr = np.mean(sheep, axis=0) if len(sheep[0]) > 0 else np.array(loc)
# gravity score (towards sheep centroid)
score_sheep = {
tuple(k): np.array(k) @ np.array(ctr - loc)
for k in [(-1, 0), (1, 0), (0, -1), (0, 1), (1, 1), (1, -1), (-1, 1), (-1, -1), (0, 0)]
}
# anti-gravity score (from tourists)
tourists = np.array(list(zip(*np.where(area_win == TOURIST))))
score_tourist = {
tuple(k): min([*[
np.array(k) @ (np.array(tourist) - loc)
for tourist in tourists
], 0])
for k in [(-1, 0), (1, 0), (0, -1), (0, 1), (1, 1), (1, -1), (-1, 1), (-1, -1), (0, 0)]
}
if any([np.sum(np.abs(tourist - loc)) < 3 for tourist in tourists]):
score_tourist[(0, 0)] = np.inf # don't stay still when tourists are around
# combine both scores
score = {
k: score_sheep[k] - fear_factor * score_tourist[k]
for k in score_sheep
}
# check
for direction, in_area in [
[(-1, 0), glob[0] > lim[0][0]],
[(0, -1), glob[1] > lim[0][1]],
[(+1, 0), glob[0] < lim[1][0]-1],
[(0, +1), glob[1] < lim[1][1]-1],
[(-1, +1), (glob[0] > lim[0][0]) & (glob[1] < lim[1][1]-1)],
[(+1, -1), (glob[0] < lim[1][0]-1) & (glob[1] > lim[0][1])],
[(-1, -1), (glob[0] > lim[0][0]) & (glob[1] > lim[0][1])],
[(+1, +1), (glob[0] < lim[1][0]-1) & (glob[1] < lim[1][1]-1)],
]:
# do not roam outside the area
if not in_area:
score[direction] = -np.inf
# the next square must be empty
elif area[x_glob+direction[0], y_glob+direction[1]] != EMPTY:
score[direction] = -100
# direction according to score
return score_to_direction(score)
The rest of the code remains the same.

This modification makes the movement way more organic. The sheep seem to have now more flexibility to avoid the tourists.
Conclusion
The movements using simple cellular automaton look organic. The answer to the question from the intro would be:
The proposed automaton can simulate movement of a sheep herd for square-shaped sheep.